É fácil supor que os momentos "aha!" da ciência vêm de resultados claros e inequívocos de testes: "Aha! A luz das estrelas curva exatamente como previsto pela teoria da relatividade geral — portanto Einstein deve estar certo!" "Aha! O número de grilos com asas mutantes é exatamente o que seria de esperar se o gene para essa característica estiver localizado no cromossoma X!" "Aha! Não importa onde eu a liberte, a esfera de aço desce a rampa com exatamente a mesma aceleração — tal como Galileu previu!"

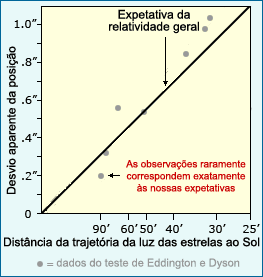
Os resultados de um dos primeiros testes à teoria geral da relatividade não deu exatamente os resultados previstos pela teoria de Einstein. Segundo a teoria, a trajetória da luz devia parecer mudar de posição dependendo da distância a que passava perto de um objeto maciço. Cada ponto no gráfico representa uma estrela.   De facto, os resultados científicos raramente são tão claros. Einstein, por exemplo, esperava um determinado grau de curvatura da luz das estrelas (1,75 segundos de arco, para ser exato), mas as observações de 1919 foram ligeiramente diferentes (1,98, 1,61 e 0,93 segundos de arco).1 E embora a genética mendeliana tenha levado os cientistas que estudavam asas de grilos mutantes a esperar que uma das suas experiências de acasalamento produzisse metade da prole normal e metade mutante, a experiência na realidade produziu 160 crias mutantes e 171 crias normais - quase metade metade, mas não exatamente.2 E claro, qualquer estudante de física que tenha tentado alguma versão da famosa experiência de Galileu pode atestar o facto de que ensaios diferentes levam a valores de aceleração ligeiramente diferentes.

O mundo real nem sempre é simples — e muitos fatores além das ideias teóricas que estão a ser testadas podem influenciar as nossas observações. Basta pensar na experiência em que uma bola rola descendo uma rampa para ver se a sua aceleração é constante. As nossas observações da velocidade e posição da bola são afetadas pela física básica do movimento — mas essas observações também são afetadas por muitos outros detalhes. O movimento do ar na sala, a precisão do nosso equipamento de medição, as variações na textura da rampa e da bola, e pequenas mudanças na forma como a bola é libertada podem afetar as nossas observações. Então, se as nossas observações não correspondem perfeitamente às expetativas geradas pelo nosso conhecimento da física, isso significa que devemos rejeitar a nossa compreensão básica da física? Ou será que isso só significa que alguns desses outros fatores levaram os nossos resultados a se desviarem um pouco do esperado? O ponto fundamental é decidir o ponto em que as nossas observações se desviam tanto das nossas expetativas que devem ser vistas como evidência contraditória. Esta é uma parte fundamental da análise e interpretação dos dados na ciência.

Mais perto do que as alternativas

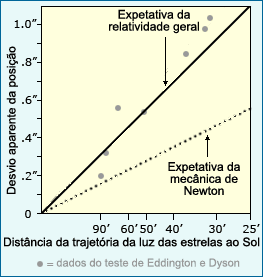
Embora os resultados de um dos primeiros testes à teoria geral da relatividade variassem um pouco, eles correspondiam às expetativas da relatividade geral muito melhor do que os da mecânica newtoniana.

Em muitos casos, a correspondência entre as observações e as expetativas é relativa. Os cientistas costumam comparar explicações alternativas que geram expetativas muito diferentes. As observações podem não corresponder exatamente a nenhum dos conjuntos de expetativas, mas se estão muito mais perto de um conjunto do que dos outros, isso pode ser visto como evidência apoiando a explicação correspondente. Por exemplo, no caso do teste à relatividade geral baseado no desvio da luz de estrelas, os investigadores compararam a mudança esperada com base na teoria de Einstein à mudança esperada com base na mecânica de Newton. O gráfico mostra os dois conjuntos de expetativas e as observações reais. É claro que, embora os dados não correspondam perfeitamente às expetativas de Einstein, eles encaixam-se nessa explicação muito melhor do que na teoria newtoniana. Isso foi interpretado como sendo evidência forte em apoio da relatividade geral.

Amostra maior, confiança maior
O exemplo da relatividade geral também ilustra outra ferramenta usada pelos cientistas para separar informação importante de influências menores: o tamanho da amostra. Muitas vezes, os fatores menores que influenciam as nossas observações não tem um padrão regular, e assim anulam-se mutuamente quando muitas observações são consideradas em conjunto. Se os cientistas que estudam a relatividade geral tivessem feito uma única observação— por exemplo, a estrela representada pelo ponto mais em baixo no gráfico que mostramos acima — eles poderiam ter concluído que Newton é que estava certo. No entanto, observações adicionais revelaram que os dados correspondiam melhor às expetativas de Einstein. O desvio dessa primeira observação do esperado com base na relatividade geral pode ter sido causado por muitos fatores diferentes - uma irregularidade na lente do telescópio ou um erro humano — mas quando muitas observações diferentes são consideradas em conjunto, o padrão dominante que aparece nos dados é óbvio. De quantas observações é que precisamos? A resposta depende, em parte, do que queremos aprender a partir dos dados. Em geral, quanto mais subtil for a diferença entre as expetativas das suposições testadas, maior o tamanho da amostra necessário. Cálculos estatísticos podem muitas vezes ser usados para descobrir o quão grande uma amostra tem de ser para se conseguir detetar uma diferença de uma certa magnitude.

Quão diferente é diferente?
Não importa até que ponto uma experiência é cuidadosamente controlada, o quão precisa é uma observação, ou quantas vezes a repetimos, os dados recolhidos numa investigação científica são suscetíveis de variar um pouco entre si e em relação às nossas expetativas. Isto é normal. A estatística pode-nos ajudar a descobrir se os nossos resultados estão dentro da gama normal de variação esperada — e quanto os nossos resultados teriam que ser diferentes das expetativas antes de devermos suspeitar que a hipótese ou teoria que estamos a testar está errada. Muitos aspetos do mundo natural envolvem incerteza inerente. Embora muitas vezes sejamos capazes de saber a probabilidade de resultados diferentes, podemos não ser capazes de prever exatamente o que vai acontecer numa situação particular. Por exemplo, em humanos, a probabilidade de dar à luz uma menina (ou um menino) é de aproximadamente 50%. (Por razões que os cientistas não compreendem inteiramente, na verdade é cerca de 49% para meninas e 51% para meninos.) No entanto, não é possível prever se uma menina ou menino vai ser concebido numa determinada gravidez natural. O que podemos é prever que, numa amostra grande e aleatória de mulheres grávidas, cerca de metade vai dar à luz meninas. Se a nossa amostra produzir 55 meninas e 45 meninos, provavelmente tal não é motivo para descartar a ideia de 50 meninas/50 meninos (ou mesmo 49/51), uma vez que alguma variação de amostra para amostra é esperada. Vários testes estatísticos diferentes (incluindo o teste do qui-quadrado) podem ajudar-nos a descobrir exatamente até que ponto as nossas observações teriam que se afastar da expetativa antes de nós devermos começar a desconfiar que uma razão de nascimentos 50/50 é uma ideia que provavelmente deveríamos rejeitar.

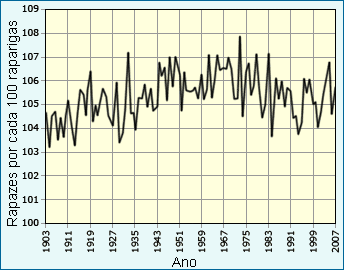
Dados coligidos ao longo de cem anos na Escócia mostram que variações de ano para ano na razão entre sexos ao nascimento se devem apenas ao acaso.

		UM AJUSTE DEMASIADO PERFEITO? Não há evidência de que Mendel tenha forjado os seus dados, mas alguns cientistas pensam que ele os possa ter distorcido sem intenção.   Os cientistas não esperam que as suas expetativas e observações correspondam exatamente, porque muitos fatores diferentes podem afetar observações e resultados de testes. De facto, quando há uma correspondência quase perfeita e sistemática entre expetativas e observações, tal é por vezes tomado como um sinal de alerta que pode ter ocorrido distorção dos dados ou mesmo fraude. Por exemplo, em 1800, Gregor Mendel realizou muitas experiências, atualmente consideradas históricas, envolvendo cruzamentos de plantas da ervilha, a fim de aprender mais sobre a hereditariedade. Ele foi o primeiro a reconhecer a existência de padrões hereditários distintos, que acabaram por ser reconhecidos como as fundações da genética moderna. O único problema? Os dados de Mendel em muitas das suas experiências parecem ser bons demais. Na década de 1930, um estatístico proeminente notou que muitos dos resultados de Mendel correspondiam às suas expetativas surpreendentemente bem. Por exemplo, num caso em que Mendel esperava uma proporção de 3:1, ele obteve proporções de 2.96:1 e 3.01:1. Estas observações (com análises estatísticas detalhadas), levou muitos cientistas a perguntarem-se se Mendel teria "embelezado" os seus dados. Ao fim de 70 anos de debate e investigação sobre a ética científica de Mendel, os cientistas e historiadores modernos não encontraram nenhuma evidência de que Mendel teria intencionalmente cometido fraude. No entanto, por causa da correspondência invulgarmente boa entre as expetativas e observações de Mendel, os cientistas continuam sem saber exatamente como é que os seus resultados acabaram por ser tendenciosos em apoio das suas ideias .3 As suspeitas levantadas sobre o trabalho de Mendel não apontaram para fraude real — mas, noutros casos, uma correspondência invulgarmente boa entre as observações e as expetativas, ou um grau de variação nos resultados dos testes invulgarmente baixo, são apenas a ponta do iceberg. Por exemplo, o investigador médico John Darsee tinha publicado vários artigos sobre medicamentos para o coração antes de os seus colegas perceberem que ele estava a rotular incorretamente os seus dados. Isso pôs os seus supervisores de sobreaviso para a existência de um problema. Eles começaram a monitorizar os resultados de Darsee mais de perto, e depressa perceberam que os seus dados eram "demasiado bons" — eles não variavam tanto quanto dados semelhantes coletados por outros. Investigações posteriores revelaram que Darsee tinha inventado dados durante 14 anos! Mais de 50 dos seus artigos e resumos foram eventualmente retratados, ele perdeu o emprego e foi impedido de receber financiamento para investigação. Resultados "perfeitos" por vezes indicam má técnica e ética científicas. Para saber mais sobre o case de Darsee, visite a página (em inglês) do National Academy of Engineering's Online Ethics Center.

Finalmente, quando se considera até que ponto uma concordância entre as observações e as expetativas é razoável, é importante relembrar que o objetivo de testes científicos é identificar a melhor explicação disponível para um determinado fenómeno — e essa explicação pode não ser perfeita. A relatividade geral, por exemplo, é atualmente a melhor explicação que temos para compreender a gravidade e o movimento de objetos massivos. É apoiada por muitas linhas de evidência e pode ser usada para fazer previsões precisas sobre fenómenos como a mudança aparente na trajetória da luz das estrelas quando passa perto de um objeto massivo. Na verdade, estudos posteriores dessa mudança por meio de satélites revelaram uma concordância muito melhor com as previsões de Einstein que as observações feitas em 1919 — mas, é claro, mesmo essas novas observações nem sempre mostram uma concordância perfeita. É provável que os desvios remanescentes em relação às expetativas sejam causados por fatores conhecidos que são simplesmente demasiado difíceis de controlar - mas não podemos descartar a possibilidade de que existe uma outra explicação, ainda melhor do que a relatividade geral, que ainda não foi descoberta!

		A variabilidade natural do mundo, e a nossa incapacidade de controlar todas as variáveis que podem afetar o resultado de um teste científico, quer dizer que os resultados de experiências raramente correspondem exatamente às nossas expetativas — mesmo quando os resultados apoiam a ideia subjacente. Os resultados dos testes científicos geralmente variam um pouco. Amostras maiores podem revelar padrões nos dados, mesmo quando os dados têm um grau elevado de variabilidade natural. Testes estatísticos podem ser usados para determinar se os resultados estão dentro da gama normal de variação de uma determinada expetativa.

		Visite o site Visionlearning (em inglês) para material avançado sobre como os cientistas quantificam a variabilidade em seus dados e usam testes estatísticos para lidar com esta variabilidade.

		Saiba mais sobre a lógica por detrás do teste à relatividade geral através da curvatura da luz das estrelas, em Testes imparciais em física: Examinando eclipses.

		Quando é que chega? Quando os alunos fazem pesquisa e atividades em laboratório, eles podem por vezes recorrer a si, como professor, para obter conselhos sobre o tamanho da amostra que é necessário. Esta é uma pergunta delicada, mas importante, para os alunos pensarem. Você pode explicar que não existe uma resposta certa. Os cientistas escolhem o tamanho das suas amostras com base em vários constrangimentos: quanto tempo e dinheiro têm para fazer o estudo, o quão grande a diferença que eles querem ser capazes de identificar (quanto menor a diferença, maior a amostra necessária), e uma série de considerações estatísticas. Você pode recomendar que os alunos comecem com uma amostra de tamanho razoável para o tempo previsto, dê uma vista de olhos nos dados para verificar se os padrões se estão a tornar percetíveis, e recolha mais dados se necessário. Este processo pode demonstrar aos alunos a importância do tamanho da amostra, dado que a interpretação dos seus resultados pode mudar quando o tamanho da amostra aumenta. Você também pode considerar a combinação dos resultados dos diferentes grupos e discutir como isso muda a confiança nas suas interpretações. Na ciência, o processo de interpretação dos dados pode ser complexo e, muitas vezes é possível ter múltiplas interpretações de um único resultado. Você pode incentivar os alunos a explorar este aspeto do processo da ciência em laboratório e em atividades onde os alunos recolhem os seus próprios dados. Peça-lhes para refletir sobre tantas explicações alternativas quanto conseguirem sobre a causa dos resultados que obtiveram - incluindo aspetos do design do teste que podem não ter funcionado como esperavam. Pergunte aos alunos como é que eles poderiam descobrir se alguma dessas explicações é mais provável que as outras.